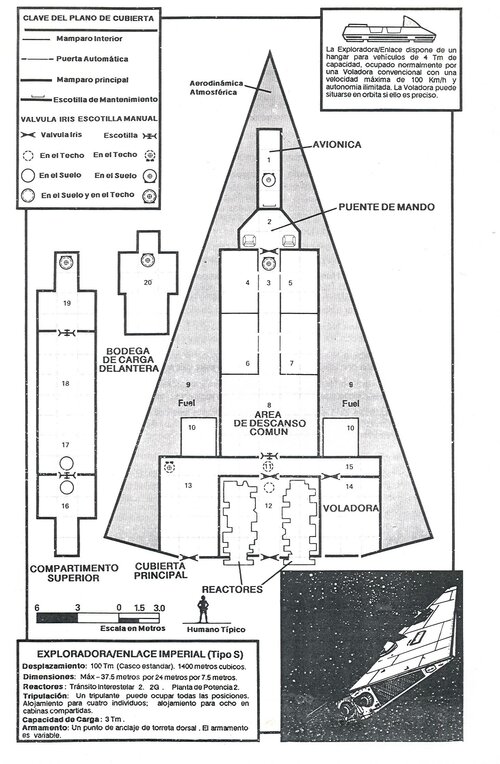
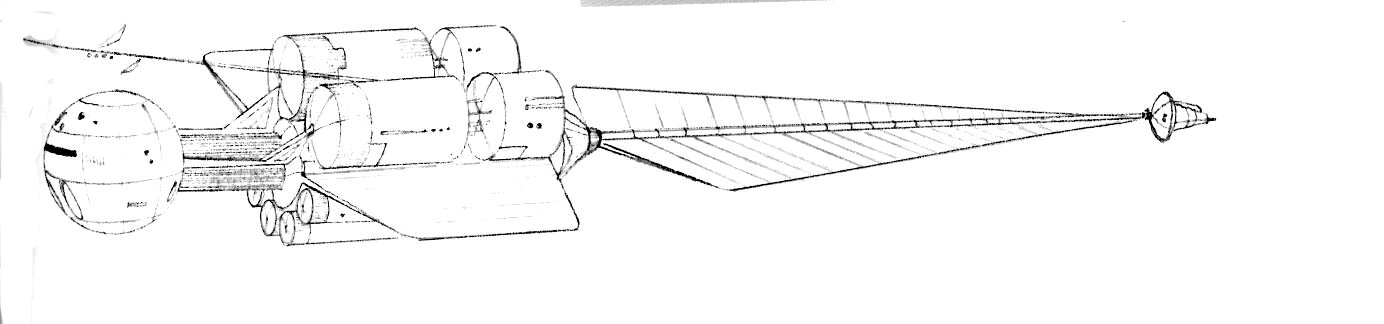
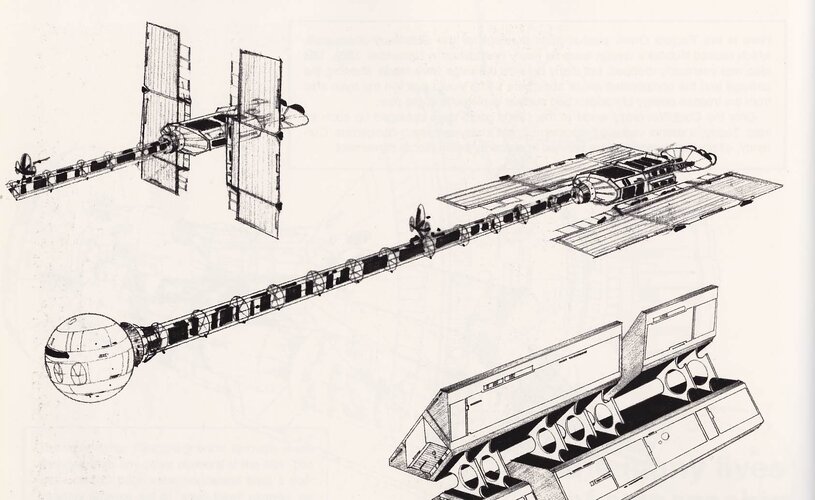
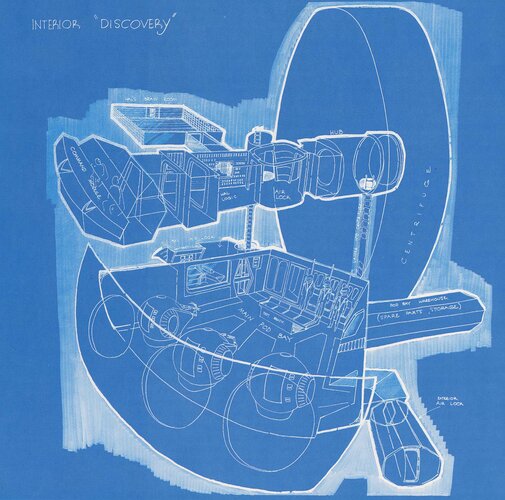
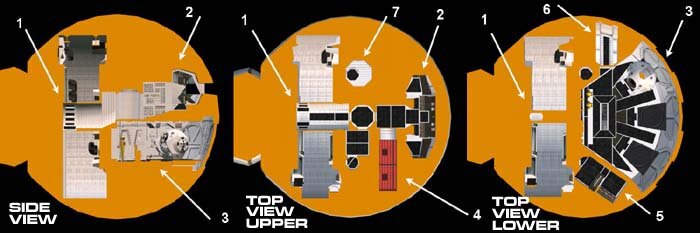
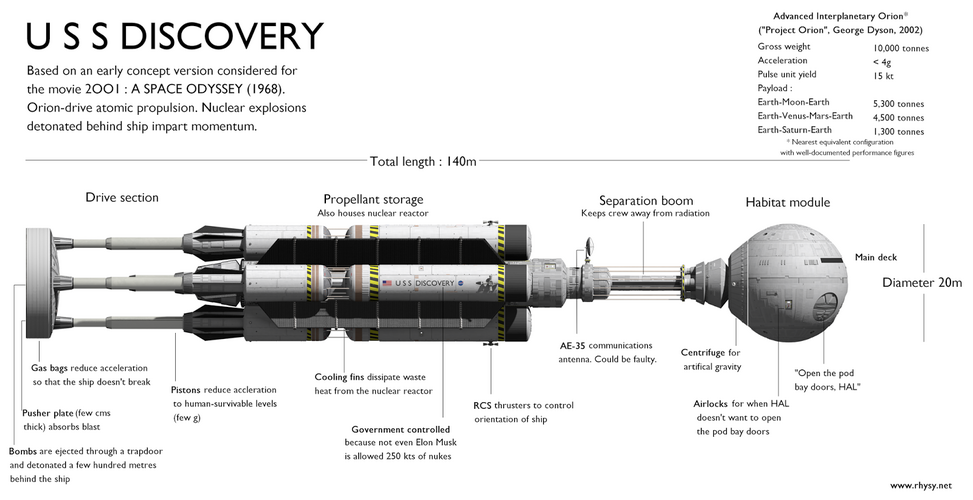
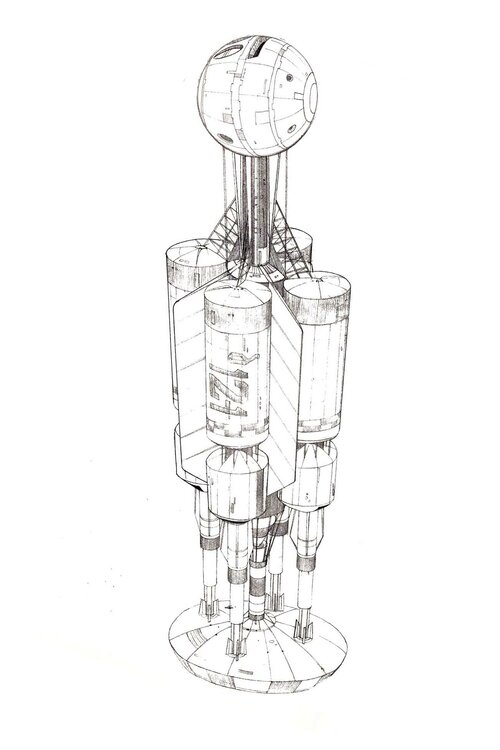
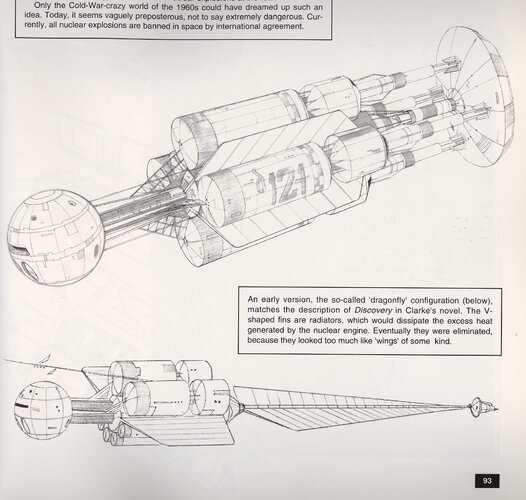
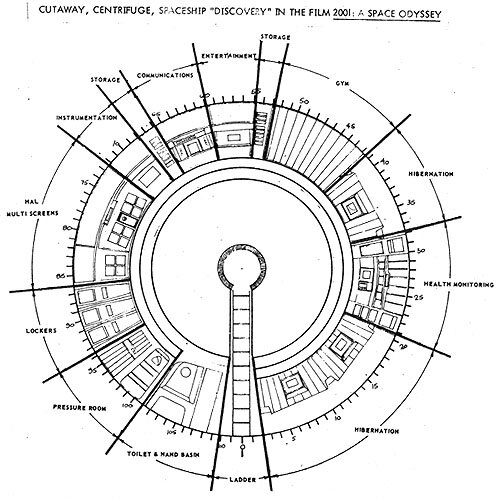
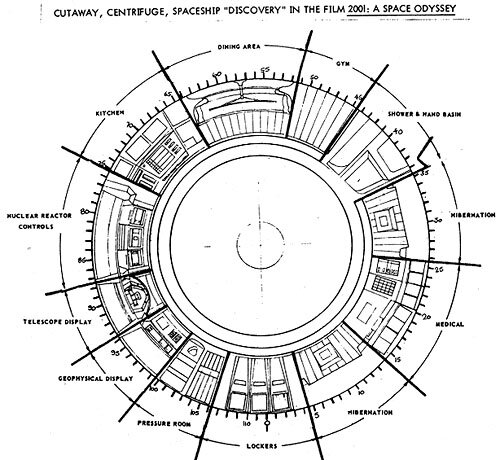
There's a kind of paradox here regarding TRL and realism. The TRL scale exists entirely within absolute realism as a one-dimensional vertical axis. A concept climbs the scale from a yell of 'Eureka!' in the bathtub as far as it can according to its inherent possibilities within the criteria of each level, which become more restrictive the higher you get.
The problem is that lower on the scale might be just a doodle, a diagram and an equation that can't be described or depicted in concrete terms which fiction, especially film, requires. Usually, that's something in appearance like our present reality of embedded in extensive worldbuilding, like the
Star Trek universe, but all that detailing, however 'real' it looks, is still fantastic.
For example, something like the Nostromo is so
dramatically convincing that you can be sure the coffee tastes terrible and Jonesy has vomited up hairballs in your bed. However, it is technically implausible because as far as we know, FTL is impossible, or at least it's not explained in a way that is plausible and detailed. On the other hand, the best NASA design reference mission plans for Mars missions are technically convincing (though obviously not at the top of the scale because they haven't been launched. Because they aren't real and are generally not realistically illustrated - simple CGI, and the subcontractors haven't yet come up with a finished user interface for the computers - but if you want to make a film of it, you have to see the actors or read about the characters using the controls (and spitting out the coffee and yelling at the cat).
Thus, something dramatically convincing has to be something you could believe you'd be able to be touched, licked, whatever. The further we project into the future, the further down the scale a spacecraft slips and the more schematic it becomes. To be convincing on both technical and dramatic grounds, we're limited to 'twenty minutes into the future' (
Max Headroom reference, there).
Going back to the TRL scale as a one-dimensional axis, I'm going to take Martin Bayer's quip about imaginary numbers seriously. These numbers aren't on the axis, they're at right angles to it. There's an explanation of how they might work here:
So if we have an axis and a radius, we have a three-dimensional conceptual space. All fictional spacecraft will look as if they're at or near ultimate TRL but radially removed. Entirely, rigorously, absolutely realistic designs can only hope to be dramatically convincing on the top few levels. If you like, a cone of possibilities rises from each step on the axis. So, how wide or narrow do we want to make the cone and how far down the axis does its point descend?
Er, that turned into a pompous academic essay. Sorry. Is that my coat?
 1.png178.6 KB · Views: 33
1.png178.6 KB · Views: 33 7d6ad896ed1d89b6af46a1ab6ddd4f20.jpg38.7 KB · Views: 21
7d6ad896ed1d89b6af46a1ab6ddd4f20.jpg38.7 KB · Views: 21 91dc61489df22f36c820bc0a9dd9babc-800.jpg138.4 KB · Views: 15
91dc61489df22f36c820bc0a9dd9babc-800.jpg138.4 KB · Views: 15 222ce467bfd91d8922067c0defe119bb.jpg96.8 KB · Views: 14
222ce467bfd91d8922067c0defe119bb.jpg96.8 KB · Views: 14 1954AuthenticBookofSpace01.jpg676.7 KB · Views: 12
1954AuthenticBookofSpace01.jpg676.7 KB · Views: 12 a977f73596e37b9e0ca1426915a624cf.jpg15.9 KB · Views: 16
a977f73596e37b9e0ca1426915a624cf.jpg15.9 KB · Views: 16 Escanear0251.jpg647.5 KB · Views: 16
Escanear0251.jpg647.5 KB · Views: 16 Escanear0315.jpg383 KB · Views: 13
Escanear0315.jpg383 KB · Views: 13 Escanear0324.jpg231.7 KB · Views: 13
Escanear0324.jpg231.7 KB · Views: 13 Escanear0332.jpg379.8 KB · Views: 10
Escanear0332.jpg379.8 KB · Views: 10