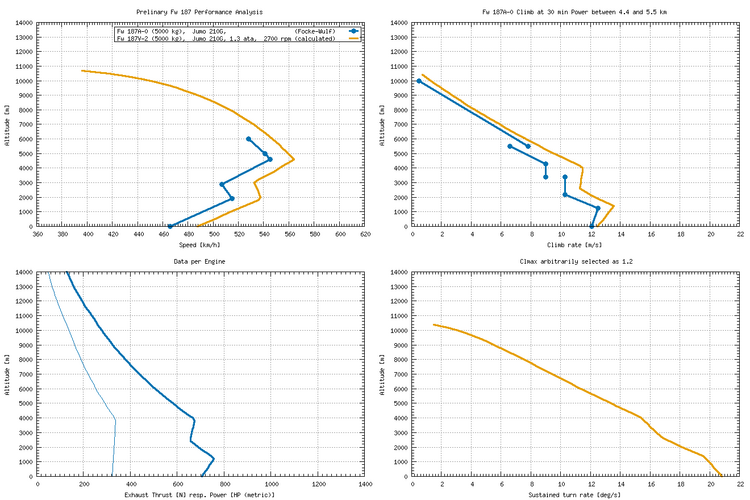
Hi Tomo,
I just had a look at Hermann's "Focke-Wulf Fw 187", and he actually reproces some pages of a Rechlin test. (Frustratingly, not all of them, but the performance pages are there, at least.)
It's for the Fw 187V2 with Jumo 210D engine, 3 m propeller diameter, at 2700 rpm, 1.28 ata, flown at 3850 kg. My guess is that this might be a bit less than the normal take-off weight ... while I don't have a weight breakdown for the V2, the A-0 is probably not all that much heavier, and it weighs in at 3723 kg empty equipped (Rüstgewicht). However, weight doesn't affect top speed much anyway ... I calculate a top speed loss of about 6 km/h when increasing weight from 3850 kg to 5000 kg.
I've prepared a diagram with the tested data, compared to a calucation of performance based on the data from the test, along with an estimate of the speeds achievable with the V2 if it had been powered by the Jumo 210G (as was used on the V3, which due to an accident didn't get to be tested at Rechlin).
I have to admit that I was a bit suprised by the big jump in performance between the Jumo 210D and the Jumo 210G, but the G actually is a much more advanced engine, featuring fuel injection and a supercharger providing a much increased full throttle height. Additionally, it was fitted with jet nozzle exhausts to exploit exhaust thrust, and (according to a remark in the V4 Baubeschreibung) also was set up to exploit the ram effect of a forward-facing intake, giving an additional boost in full throttle height that resulted in a yet higher absolute top speed.
The (two-seater) V4 actually was a bit slower than the V2 would have been, according to my calculations, but I guess that only shows you can't just add a second crew member to a single-seater design without sacrificing a bit of performance.
Compared to the 564 km/h @ 4600 m I calculated for the single-seater at 5000 kg flying weight, the Focke-Wulf number for the two-seater with the same engines at the same weight is 545 km/h @ 4600 m, or a loss of about 20 km/h top speed.
Here's the diagram:

Some notes: The Rechlin test data did not feature the characteristics points, only one value at each full kilometer height, so I didn't draw a line through the points. The Rechlin-measured top speed of 501 km/h @ 3000 m was achieved at 1.26 ata instead of the maximum of 1.28 ata, so I figure the real top speed was probably about 502 km/h @ 2800 m.
My calculations deviate from Rechlin data in low supercharger gear, and while I'm low in top speed, I'm high in climb. That makes no sense at all ... if I had only the speed graph, I'd suspect some peculiarity of low supercharger gear operation, such as automatically engaged carburettor heating or something, but as the climb graph is off in the opposite sense, I think not all of the Rechlin data points are actually sensible. I suspect their climb data is too high for low altitude ... nothing serious, there are small glitches like that in a lot of the historic data sets, from all sides.
(If 3850 kg isn't the full normal take-off weight, the climb rate should actually be lower anyway, if one adheres to the convention on showing the climb rate normal take-off weight for comparison purposes.)
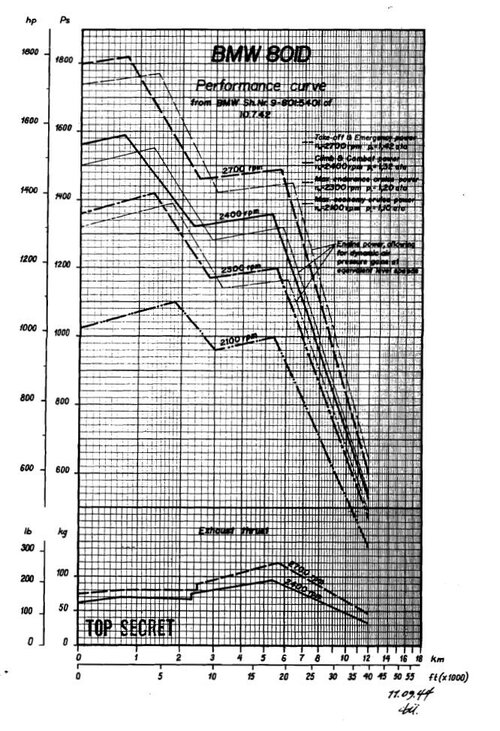
I have two slightly different power charts for the Jumo 210D, and they are for 1.3 ata while the Rechlin test was run at 1.28 ata. I'm also not entirely sure of the reduction gear ratio, which affects top speed above full throttle height ... a page from a pre-war catalogue shows a gear ratio of 0.628, but the engine portrayed there is referred to as Jumo 210Da, and descrived as having a 3.4 km rated altitude, while the one used on the Fw 187V2 has a full throttle height of just 2.8 km.
Regards,
Henning (HoHun)
Goes without saying that I'd just love to see flight tests of many, many pre-war British and German aircraft
I just had a look at Hermann's "Focke-Wulf Fw 187", and he actually reproces some pages of a Rechlin test. (Frustratingly, not all of them, but the performance pages are there, at least.)
It's for the Fw 187V2 with Jumo 210D engine, 3 m propeller diameter, at 2700 rpm, 1.28 ata, flown at 3850 kg. My guess is that this might be a bit less than the normal take-off weight ... while I don't have a weight breakdown for the V2, the A-0 is probably not all that much heavier, and it weighs in at 3723 kg empty equipped (Rüstgewicht). However, weight doesn't affect top speed much anyway ... I calculate a top speed loss of about 6 km/h when increasing weight from 3850 kg to 5000 kg.
I've prepared a diagram with the tested data, compared to a calucation of performance based on the data from the test, along with an estimate of the speeds achievable with the V2 if it had been powered by the Jumo 210G (as was used on the V3, which due to an accident didn't get to be tested at Rechlin).
I have to admit that I was a bit suprised by the big jump in performance between the Jumo 210D and the Jumo 210G, but the G actually is a much more advanced engine, featuring fuel injection and a supercharger providing a much increased full throttle height. Additionally, it was fitted with jet nozzle exhausts to exploit exhaust thrust, and (according to a remark in the V4 Baubeschreibung) also was set up to exploit the ram effect of a forward-facing intake, giving an additional boost in full throttle height that resulted in a yet higher absolute top speed.
The (two-seater) V4 actually was a bit slower than the V2 would have been, according to my calculations, but I guess that only shows you can't just add a second crew member to a single-seater design without sacrificing a bit of performance.
Compared to the 564 km/h @ 4600 m I calculated for the single-seater at 5000 kg flying weight, the Focke-Wulf number for the two-seater with the same engines at the same weight is 545 km/h @ 4600 m, or a loss of about 20 km/h top speed.
Here's the diagram:
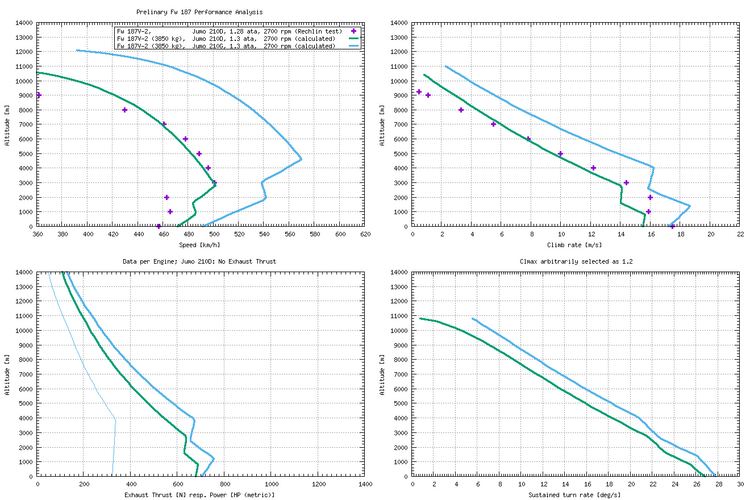
Some notes: The Rechlin test data did not feature the characteristics points, only one value at each full kilometer height, so I didn't draw a line through the points. The Rechlin-measured top speed of 501 km/h @ 3000 m was achieved at 1.26 ata instead of the maximum of 1.28 ata, so I figure the real top speed was probably about 502 km/h @ 2800 m.
My calculations deviate from Rechlin data in low supercharger gear, and while I'm low in top speed, I'm high in climb. That makes no sense at all ... if I had only the speed graph, I'd suspect some peculiarity of low supercharger gear operation, such as automatically engaged carburettor heating or something, but as the climb graph is off in the opposite sense, I think not all of the Rechlin data points are actually sensible. I suspect their climb data is too high for low altitude ... nothing serious, there are small glitches like that in a lot of the historic data sets, from all sides.
(If 3850 kg isn't the full normal take-off weight, the climb rate should actually be lower anyway, if one adheres to the convention on showing the climb rate normal take-off weight for comparison purposes.)
I have two slightly different power charts for the Jumo 210D, and they are for 1.3 ata while the Rechlin test was run at 1.28 ata. I'm also not entirely sure of the reduction gear ratio, which affects top speed above full throttle height ... a page from a pre-war catalogue shows a gear ratio of 0.628, but the engine portrayed there is referred to as Jumo 210Da, and descrived as having a 3.4 km rated altitude, while the one used on the Fw 187V2 has a full throttle height of just 2.8 km.
Regards,
Henning (HoHun)