Design Challenge: around the world from east to west or pole to pole

N

Nicknick

ACCESS: Top Secret
Joined
12 September 2021
Messages
936
Reaction score
636
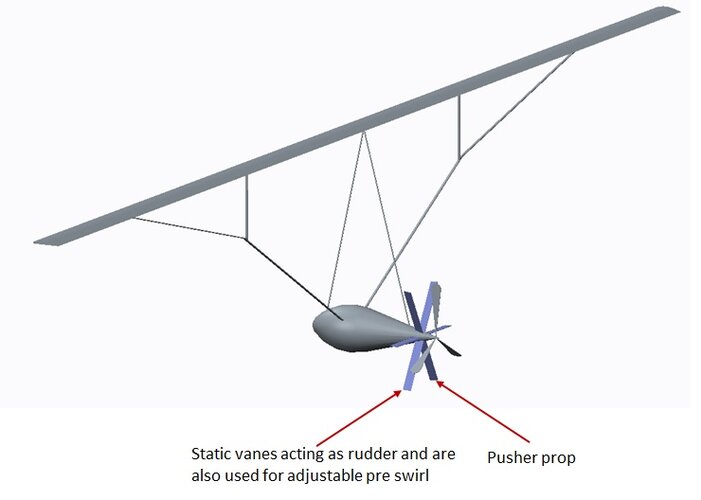
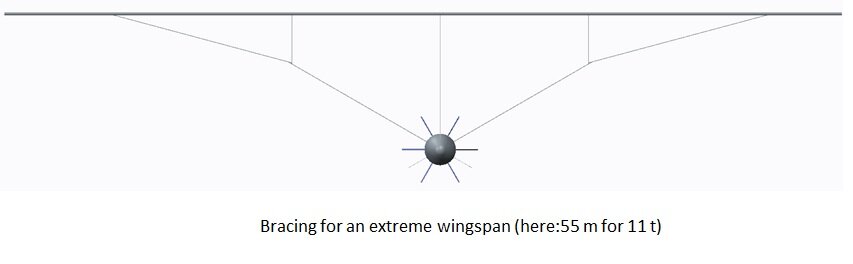
I thought it would be time for a new design challenge, the around the world plane from pole to pole or westwards against the jet streams or anything other more difficult than that what the voyager has done before…

Before I come out with a design proposal, I will explain my idea of the flight profile. Of course, this is an idealized idea and reality can and will disturb it (weather, traffic, etc.). So, I will explain how it would work in an ideal world. It is clear, that this super long range aircraft will have a drastically changing total mass during the flight. For simplicity reasons, I declare the mass ratio 1 as the mass which allows for flying at an optimal angle of attack with max efficiency power at sea level. The starting mass could possibly be a bit higher (flying behind the power curve) and is set to 1.1. The fuel will be empty (a small reserve should be kept) at a mass ratio of 0.2 (might be overly optimistic…). For maximum efficiency, the plane should always fly with the best angle of attack and for most of the time with constant engine power. Of course, the engine should run in the point of best efficiency, except in the first part of the flight (mass ratio >1) where we allow it to run with a slightly higher rpm to reach more power.

Below a mass ratio of 1, the plane will become faster and to keep the optimum angle of attack, the ratio of lift and thrust must be kept constant. With a constant engine power, the plane must fly higher and become faster. If the mass ratio is down to 0.5, the plane will fly in 1/8 of the air density with twice the speed and half the mass, compared to mass ratio 1. The lift is:

L=C*2²*1/density

So with V2 = 2* V1 and density 2 = 1/8 * density 1 =>

L2 = ½ L1

Since we fly with a constant angle of attack, the drag is proportional to the lift

Fd2 = ½ Fd1

Thrust power:

P2=Fd2*V2 = Fd2*V1 = P1

So we see, the power can be kept constant with a declining mass ratio. It is clear, that the design should be able to fly quite slow (250 – 300 km/h) at sea level (mass ratio 1) and needs to climb really high (16500 m for a mass ratio of 0.5). With two stage turbocharging, we could even fly higher, so we continue with this up to a mass ratio of let’s say 0.4. With that mass ratio we reached the maximum height and speed (Mach number limitations) and need to change our strategy. In the next flight phase we continue to fly with a constant angle of attack, but we will reduce speed and engine power while maintaining the height. To ease calculations, we will do so, until we reach a mass ratio of 0.2. Let’s check how it works out for this point:

We will need only half the lift and lift is proportional to the square of the speed, so:

V3=1/2² *V2

With a constant angle off attack, thrust force is proportional to the lift, so it is also down to

Fd3 = 1/2 Fd2

The required thrust power will be:

P3 = P2 * Fd3* V3 = 0,039 * P2

This relatively low engine power will reduce efficiency, but to be honest, a mass ratio of 0.2 would be very low and probably unrealistic, I choosed it mainly because to simplify the diagrams.

The last part of the flight will be a powerless glide with the best angle of attack until we reach the landing side.

I made a diagram with the mass ratio vs. air density, this might be a bit unusual, but it allows to use straight lines instead of complex curves which would be required if the altitude would be used.

I would like to see design proposals for such a plane and will contribute something by myself….
 

Attachments

  • flight_profile.JPG
    flight_profile.JPG
    45.4 KB · Views: 33
Last edited:
You must be assuming jet power, because Voyager's speed didn't increase that much over the course of their flight.
 
No, I'm thinking on an ignition jet piston engine powered with Jet-A and LNG (basically those engines are Diesel engine which uses the fuel injection to ignite the lean gasous mixture). The combination of the higher gravimetric energy content and the high efficiency will give about 40 % more power per kg fuel as AVGAS with Otto engines.

Voyager was lacking cabin pressurisation and turbocharging, that's why they couldn't fly higher. They also used anoter strategy, instead of constant engine power with increasing speed and height, Burt Rutan went for variable engine power (by switching one engine off in the second half of the flight) and lesser gain in speed and height.

Edit:
The Voyager engines were optimized with a high compression ratio and archieved a break specific fuel consumption of 0.375 lb/hph (https://www.sae.org/publications/technical-papers/content/871042/). The LNG/Diesel engines will consume 25 % less mass for the same amount of power.
 
Last edited:
Thanks, intresting, but the boundary conditions are different. In the Brequet Equation, a constant thrust is considered and not a constant power. Also no large variation in speed is allowed and jets tend to fly with high Mach numbers quite from the begining.

I propose a piston engine propeller driven plane with a low speed at the beginning of the journey (200 - 250 km/h) which will more than double until the maximum height is archieved.
 
Nicknick said:
No, I'm thinking on an ignition jet piston engine powered with Jet-A and LNG (basically those engines are Diesel engine which uses the fuel injection to ignite the lean gasous mixture). The combination of the higher gravimetric energy content and the high efficiency will give about 40 % more power per kg fuel as AVGAS with Otto engines.
Click to expand...
Hrm. That... might work?

I mean, yes, a diesel aircraft engine works just fine. I'm not sure that LNG is a good aircraft fuel, depends on density of the fuel and bulk of the tanks.


Nicknick said:
Voyager was lacking cabin pressurisation and turbocharging, that's why they couldn't fly higher. They also used anoter strategy, instead of constant engine power with increasing speed and height, Burt Rutan went for variable engine power (by switching one engine off in the second half of the flight) and lesser gain in speed and height.
Click to expand...
I don't think that's right, but it's been a long time since I read the book. The front engine was basically there for climb power when fully loaded, and was then shut off after they arrived at 10kft. Then they restarted the engine later for something. Like I said, been way too long since I read the book.

Voyager's fuel load was 7450lbs of 100LL avgas, for a fuel fraction of 0.768.
 
Well, I don't see it as a contradiction, as said, the real world will sometimes require compromises. Without any disturbance, the second engine would have stayed unused for the later part of the flight (might have been more or less than 50%), but they needed to restart is because of temporary troubles with the fuel supply on the rear engine and another time to fly above the weather.

I would like to focus on the flight profile before I make a proposal for the design, but LNG could enable an efficient package with a very special approach. LNG boils off without residues, this would enable to use some areas in the plane for fuel storage in the beginning and for other puposes later in the flight. The sleeping compartment could be used as tank and also the cooling system for high altitudes could be integrated in a closed chamber which would be flooded with LNG in the first part of the flight.
 
Last edited:
Nicknick said:
Well, I don't see it as a contradiction, as said, the real world will sometimes require compromises. Without any disturbance, the second engine would have stayed unused for the later part of the flight (might have been more or less than 50%), but they needed to restart is because of temporary troubles with the fuel supply on the rear engine and another time to fly above the weather.

I would like to focus on the flight profile before I make a proposal for the design, but LNG could enable an efficient package with a very special approach. LNG boils off without residues, this would enable to use some areas in the plane for fuel storage in the beginning and for other puposes later in the flight. The sleeping compartment could be used as tank and also the cooling system for high altitudes could be integrated in a closed chamber which would be flooded with LNG in the first part of the flight.
Click to expand...
Yikes, do not like that! You'd have to blow so much ventilation air into that space before it could be safely entered, let alone occupied long term. I'm talking over 10 half-lives (changing half the air in the volume at least 10 times), plus using a Draeger to check for the total gas concentrations while wearing a forced air respirator... Can be done, but I heartily discommend allowing people inside an LNG tank.

Other uses are fine, just no people in LNG tanks, or LNG in the people tanks!

=====
LNG is 0.5kg/L, while jet fuel is 0.8kg/L, so it's a bit bulkier that way, and then you need the mild cryo insulation or vacuum flasks because it's stored at -165degC/-260degF, a bit colder than dry ice. Way better than hydrogen, but that bar is so low it's a trip hazard.

I suspect that running those engines on pure Jet A would be better in terms of fuel volume in the aircraft, unless there's a lean burning trick involved that reduces the amount of fuels burned by more than half in cruise.
 
Methane does no harm to humans and it doesn't even smell. I agree, a large amount of venting will be needed so supress any fire hazzard, this could be done by letting the engine inhale air from that area. Gas warning systems should be applied, those are widly available and not very fancy stuff.

Running on pure Jet-A would be better from a volumetric standpoint, but LNG offers 14 % less energy specific weight and the storing trick, which can't be done with smeary gazoline.

LNG will be cooled by boiling off and the gasous Methane will be inhaled by the engine, so a large amount of isolation is not required. The biggest issue in my view is icing on the fuselage, this should be prevented by some degree of isolation. Aerogel is a very fine solution for lightweight isolation, this could be applied here and wouldn't affect the mass significantly.
 
Nicknick said:
Thanks, intresting, but the boundary conditions are different. In the Brequet Equation, a constant thrust is considered and not a constant power. Also no large variation in speed is allowed and jets tend to fly with high Mach numbers quite from the begining.

I propose a piston engine propeller driven plane with a low speed at the beginning of the journey (200 - 250 km/h) which will more than double until the maximum height is archieved.
Click to expand...
The Breguet equation dates back to the 1920s, see for example https://ntrs.nasa.gov/api/citations/19930091302/downloads/19930091302.pdf, so it was explicitly developed for low speed piston engine propeller driven planes, even though it applies to jets as well. If you're aiming at a plane that has global (antipodal) range, why do you seemingly want to unnecessarily introduce artificial constraints on the flight profile?
 
thanks, I need some time to read and understand all 18 pages, so right now I just read the very beginning and it is totally in line with what I have written above (No, Im not suprized, that this wasn't entirely new....).

I need to check all of their assumptions and I guess I will somewhere find the same as I have drawn above.

For practical reasons, nobody at that time will have considered a prop driven plane at more than 15.000 m a realistic option. Also a highly variing speed is not really practical for airliners.

There is more than one formula for maximum range, because it depends of the boundary conditions. I go for flying at best L/D ratio (as they do) in combination with a constant engine power for best efficiency which they might also do on one of the pages. I just have to go through it, but it might also be the case, that this scenario was rejected because of lacking practibility at the time.

I'm not introducing artificial constrains, I do the opposite and take them away, no constant speed and no constant altitude.

In fact, I do the same as Otto did with the Celera, so even here I didn't invent anything new...

I took a second look on the paper, I havne done all the math, but what I find so far:

- The simplest Form of the Brequet equation gives you the range which can be archieved depending on the mass ratio (fueled and emtied) when flying with optimum L/D ratio all the time. This is, what everyone want's to archieve, including me....
It does not tell you how to do it.

-All the calculations in this paper were done for a constant altitude and fit to that what I've drawn in the third part of the flight.

-This paper takes engine efficiency into account and the effect of decreasing efficiency with low engine loads. I totally agree on that, and therefore my aim is to keep the engine power constant by climbing and increasing speed instead of flying ever slower with constant altitude.
 
Last edited:
Nicknick said:
Methane does no harm to humans and it doesn't even smell. I agree, a large amount of venting will be needed so supress any fire hazzard, this could be done by letting the engine inhale air from that area. Gas warning systems should be applied, those are widly available and not very fancy stuff.
Click to expand...
In addition to the fire hazard (and explosion hazard if the fumes are between 4% and 15% of the volume), Methane is a general asphyxiant.

"Inhalation (Breathing): Inhalation of large quantities of LNG vapors may cause central nervous
system depression with nausea, headache, dizziness, vomiting, and incoordination. LNG and
associated vapor is a simple asphyxiant and may cause loss of consciousness, serious injury, or
death by displacing air, thereby resulting in insufficient oxygen to support life. Prompt medical
attention is strongly recommended in all cases of inhalation overexposure. Rescue personnel
should be equipped with a self‐contained breathing apparatus. Remove inhalation victims to
fresh air quickly. If inhalation victim is not breathing, ensure that their airways are open and
administer cardiopulmonary resuscitation (CPR). If necessary, have a trained person administer
air or oxygen once breathing is restored. Seek immediate medical treatment."​
Source: https://www.pgworks.com/uploads/pdfs/LNGSafetyData.pdf

Nicknick said:
Running on pure Jet-A would be better from a volumetric standpoint, but LNG offers 14 % less energy specific weight and the storing trick, which can't be done with smeary gazoline.

LNG will be cooled by boiling off and the gasous Methane will be inhaled by the engine, so a large amount of isolation is not required. The biggest issue in my view is icing on the fuselage, this should be prevented by some degree of isolation. Aerogel is a very fine solution for lightweight isolation, this could be applied here and wouldn't affect the mass significantly.
Click to expand...
You're still talking about storing a -165degC liquid for 10 days or so in the aircraft (based on Voyager's flight time), the tanks are going to need insulation.
 
Nicknick said:
thanks, I need some time to read and understand all 18 pages, so right now I just read the very beginning and it is totally in line with what I have written above (No, Im not suprized, that this wasn't entirely new....).

I need to check all of their assumptions and I guess I will somewhere find the same as I have drawn above.

For practical reasons, nobody at that time will have considered a prop driven plane at more than 15.000 m a realistic option. Also a highly variing speed is not really practical for airliners.

There is more than one formula for maximum range, because it depends of the boundary conditions. I go for flying at best L/D ratio (as they do) in combination with a constant engine power for best efficiency which they might also do on one of the pages. I just have to go through it, but it might also be the case, that this scenario was rejected because of lacking practibility at the time.

I not introducing artificial constrains, I do the opposite and take them away, no constant speed and no constant altitude.
Click to expand...
The Breguet equation is applicable to a wide range of flight conditions, see for example https://ntrs.nasa.gov/api/citations/19720012358/downloads/19720012358.pdf, and neither flight speed nor flight altitude are explicitly factors in it, although L/D and specific fuel consumption are certainly influenced by those parameters. It is however true that this equation is only valid for cruise conditions, so that the ascent and descent legs have to be considered separately. I would however strongly advise against even considering a powerless glide for the final descent and landing. What is your exact definition/understanding of the best/optimum angle of attack postulated above?
 
@Scott Kenny : For any impact in health, really high concentrations are neccessay, were talking about % and not ppm. Also I suggest to use almost pure Methane and avoid Propane which has some effect on the brain (some folks use Propane filled cream bottles to get high....).

I agree, the plane needs some isolation and Aerogel is the right stuff to do it https://en.wikipedia.org/wiki/Aerogel

@martinbayer : I totally agree with the Brequet equation (I guess 1 and 2 in the paper are Brequet equations), it gives an upper limit of what is possible but it doesn't tell you how to do it, other than by flying with best L/D and an high mass ratio and fuel with an high energy content. Thats exactly what I'm focussing on.

There is more than one way in theory, you could eg. fly slower at constant altitude when the plane gets lighter, or you can fly faster with increasing altitude, both ways allow a constant optimum L/D ratio.

In my graph, you will find (as Did Otto with the Celera and I'm inspired from that) that cruise at constant altitude ist not the main part of the flight, most fuel is used in the much longer climp to maximum height. In both cases, the optimum L/D ratio is kept.

Also inline with youre paper, right at the beginning when the plane is very heavy, the best L/D ratio can not be kept and loading less fuel to reduce the weight wouldn't increase range.

As said, this should be the ideal flight sheme and will be compromized by reality.
 
Last edited:
Thanks, such programs would be helpfull for detailed planing and taking account of prop efficiency, compressibility, weather and so on. As said, I tried to take away as many constrains as possible, therefore the proposed solution is not practical for any airliner. A record attempting airplane might get some priviliges and fly with a long constant climp, or someone might be willing to risk his licencens for a record...

You are welcome to check my diagram and estimations for any mistakes.
 
Can you drop stuff off along the way? Say a secondary engine and fuel tank for takeoff, and external fuel tanks and possibly wing tips.
 
Thought about that, but since the voyager didn't use that option (well, exept the wingtips....), I guess it might be forbitten for an official record.

I used the Brequet formula as given in the paper by Martin. For the fuel consumption I choosed 170 g/kwh (=0,28 p/hph) which is a very low figure, but totally realistic for more than 90% Methan and only 10% Diesel/Jet-A and an efficiency of 44 %. For L/D I used 25 and for the weight ratio 3.67 this resulted in more than 37.000 miles. I will do it with metric dimensions tomorrow...
 

Attachments

  • Brequet_imperial.JPG
    Brequet_imperial.JPG
    20.4 KB · Views: 28
Last edited:
Scott Kenny said:
In addition to the fire hazard (and explosion hazard if the fumes are between 4% and 15% of the volume), Methane is a general asphyxiant.

"Inhalation (Breathing): Inhalation of large quantities of LNG vapors may cause central nervous​
system depression with nausea, headache, dizziness, vomiting, and incoordination. LNG and​
associated vapor is a simple asphyxiant and may cause loss of consciousness, serious injury, or​
death by displacing air, thereby resulting in insufficient oxygen to support life. Prompt medical​
attention is strongly recommended in all cases of inhalation overexposure. Rescue personnel​
should be equipped with a self‐contained breathing apparatus. Remove inhalation victims to​
fresh air quickly. If inhalation victim is not breathing, ensure that their airways are open and​
administer cardiopulmonary resuscitation (CPR). If necessary, have a trained person administer​
air or oxygen once breathing is restored. Seek immediate medical treatment."​
Source: https://www.pgworks.com/uploads/pdfs/LNGSafetyData.pdf


You're still talking about storing a -165degC liquid for 10 days or so in the aircraft (based on Voyager's flight time), the tanks are going to need insulation.
Click to expand...
One way to avoid most of these problems is to install a water-proof/gas-proof/fuel-proof “condom” in the first fuel tank. After the first 4 or 5 hours of climb, you remove a flexible (tension only) bulkhead and invert the condom/fuel bladder. Shove your legs inside and take a nap.
 
Please note, they talkt about inhaling large quantities, not a few molecules. But anyway, the sleeping compartment would have to be sealed against the cockpit in a safe manner as long as there is Methan inside, this could be done with the large "Condome or a sealed door. I still believe, venting is not really criticall and can be done propable by letting the engine suck all the air for combustion.

What I dislike about the condom idea is, that there will be remainings inside the condom and you have to detach it manually, therefor the danger of getting on contact with a larger amount of gas is higher than by simply venting the compartment.
 
Last edited:
So here is my idea, a kind of fixed wing glider. For obvious reasons, a ultra-long range plane should have a maximum relation of fuel mass vs. empty mass so we need to build it as light as possible. The lightest existing structures for motorized flights are in fact Paragliders. The suspension allows to eliminate almost any bending in the wing, so that it can be inflatable. I wouldn‘t go so far, since those wings are not very effective, so I would like to keep the suspension but with a reduced number of wires and use a fixed wing with an extreme wingspan. The suspension wires will cause some drag but reduce the wing bending moment to a minimum. A combination of fixed struts in the upper part and flexible wires in the lower part is also possible.

A glider design would also allow gravity control which simplifies the wing structure since no flaps are used. The stability in gliders can be achieved without a downforce producing tail, the CG is in front of the center of lift and the opposing moment is induced by the thrust and the drag of the wing (showed in the pics).

The take-off will be quite tricky, I would prefer to start and land on a frozen lake, so that runners can be used instead of wheels which saves space and weight. Also, the runway length can be much longer than for any regular runway and the cold temperatures will also help. For the start, the wing should initially be attached to the fuselage by a strut and released when the speed is increasing. The wires need to be wound up on a drum and slowly getting released to bring the wing in the flying position (shurly not an easy task…). I admit, I haven’t found a solution which I really like so far…

The fuel (mainly LNG) will be stored in the fuselage. As said, some compartments of the fuselage will be filled with liquid Methane before they are emptied and used for other purposes. This could be the sleeping compartment, the high altitude cooling system, the storing room for retractable runners or wheels and maybe even a toilet.

The compartment is fully pressurized (including the tanks and maybe even the engine compartment shall be able to act as a rescue boat or shelter in case of an emergency landing. In case of an emergency situation, the wing should be detached and a rescue parachute shall be used. Also a fast release system for the fuel will be recommended.

A combined adjustable pre swirl and rudder device is foreseen to enable a highly variable plane speed and rudder control without an additional rudder. The actuation of the pre swirl device is quite complex, maybe the best way is to control each blade by an individual electric motor.

To match my graph, I estimate a starting weight of 11 t and an empty weight of 2.5 t which is the same ratio as Burt Rutans voyager, but I have no experiences at all in airplane design, so this is just guessing. I believe, the structural weight could be lighter than that of the voyager, but the pressurisation and robust fuselage design will add some weight.

ULR_plane.jpg Front.JPG
 

Attachments

  • balancing of moments.jpg
    balancing of moments.jpg
    37.2 KB · Views: 24
riggerrob said:
One way to avoid most of these problems is to install a water-proof/gas-proof/fuel-proof “condom” in the first fuel tank. After the first 4 or 5 hours of climb, you remove a flexible (tension only) bulkhead and invert the condom/fuel bladder. Shove your legs inside and take a nap.
Click to expand...
It's a -165degC liquid. You'd need to have that whole tank boil and come up to 20degC before it was safe to mess with that condom.



Nicknick said:
Please note, they talkt about inhaling large quantities, not a few molecules. But anyway, the sleeping compartment would have to be sealed against the cockpit in a safe manner as long as there is Methan inside, this could be done with the large "Condome or a sealed door. I still believe, venting is not really criticall and can be done propable by letting the engine suck all the air for combustion.

What I dislike about the condom idea is, that there will be remainings inside the condom and you have to detach it manually, therefor the danger of getting on contact with a larger amount of gas is higher than by simply venting the compartment.
Click to expand...
And you're talking about opening up a space that contained pure fuel to human occupation.

It will take a minimum of 10 ventilation half-lives to get the concentration down to ppm levels before you can think about sticking a human inside. Probably 24hrs or so. We had much bigger tanks on the subs, and they took 3-5 days of ventilation before they were safe to enter without a forced air respirator.

Please, go look up Confined Space Entry protocols and Gas Free testing.
 
No, the space would be vented by one opening to the athmosphere and another one to the engine intake. The engine(s) with estimated 500-700 kW will consume about 10 m³ air per minute, so it really takes just a short time to vent a compartment of about 2 m³. There is no hurry to do so and after one hour venting the volume would have been replaced 300 times.

I would be suprized, if the sub was powered by LNG, with fuel oil you will have a film sticking on the walls which will slowly evaporate. With Methane or LNG as fuel, everything will turn to gas and no wall fim will occure, hence you don't have the same problems as in a fuel oil tank.

BTW: I read a paper about pre cautions when handeling LNG (https://www.dena.de/fileadmin/dena/...FAQ_Unfallhilfe_Bergen_bei_LNG-Fahrzeugen.pdf), according to this paper, it is neither toxic nor corrosive or an acid. The only "danger" is, that it lowers the Oxygen content in the air, as any other gas exept Oxyen will do. Another point is, that breathing extremly cold gases isn't good for the lungs but these two problems are allready uncritical with very little venting.
 
Last edited:
Nicknick said:
No, the space would be vented by one opening to the athmosphere and another one to the engine intake. The engine(s) with estimated 500-700 kW will consume about 10 m³ air per minute, so it really takes just a short time to vent a compartment of about 2 m³. There is no hurry to do so and after one hour venting the volume would have been replaced 300 times.

I would be suprized, if the sub was powered by LNG, with fuel oil you will have a film sticking on the walls which will slowly evaporate. With Methane or LNG as fuel, everything will turn to gas and no wall fim will occure, hence you don't have the same problems as in a fuel oil tank.
Click to expand...
I was actually referring to the seawater trim tanks that needed 3-5 days of ventilation before access.



Nicknick said:
BTW: I read a paper about pre cautions when handeling LNG (https://www.dena.de/fileadmin/dena/...FAQ_Unfallhilfe_Bergen_bei_LNG-Fahrzeugen.pdf), according to this paper, it is neither toxic nor corrosive or an acid. The only "danger" is, that it lowers the Oxygen content in the air, as any other gas exept Oxyen will do. Another point is, that breathing extremly cold gases isn't good for the lungs but these two problems are allready uncritical with very little venting.
Click to expand...
Yes, the safety concerns are oxygen displacement and low temperatures. And a risk of explosions while ventilating the tanks until the fuel concentration is below 4%, but that should only last a few minutes. Might want to use exhaust gas to inert the tank until the fuel concentration is under 4% before you start putting air into the tank.
 
Quite off topic, but I would be intrested why is that so? I guess, they are emptied with compressed air, but it might also be a very secret special gas...

The idea with the exhaust gas is a good one, exept for the sleeping compartment there it will leave some smell behind...
 
Nicknick said:
Quite off topic, but I would be intrested why is that so? I guess, they are emptied with compressed air, but it might also be a very secret special gas...
Click to expand...
The trim tanks? Apparently there's a risk of H2S and some other odd gasses built up, including hydrocarbons. Because there's always hydrocarbons in the water especially around an anchorage.
 
How about reversing the "condom" idea and instead use bladder thanks in the living area that deflate/collapse as they are depleted, potentially supported by atmospheric overpressure in the compartment(s). With such an arrangement there is no need to invert the flexible tank inside out or remove a bulkhead. With some residual propellant in gaseous form at room temperature, you might even have a ready made "air" mattress :). A challenge would be finding a bladder fabric or other material that maintains flexibility at low fuel temperatures.
 
The low temperature will really make the blatter idea very demanding. It might feel wrong to sleep in a fuel tank, but Methan really isn't that dangerous and it will disapear without a trace.

Anway, flooding the sleeping compartment is not the main aspect of the whole idea...
 
Nicknick said:
The low temperature will really make the blatter idea very demanding. It might feel wrong to sleep in a fuel tank, but Methan really isn't that dangerous and it will disapear without a trace.

Anway, flooding the sleeping compartment is not the main aspect of the whole idea...
Click to expand...
If you filled every OTHER void space in the airframe with LNG tankage and left a decently sized (Minimum of 40"/1m diameter) crew space open, that would probably be better for everyone's peace of mind.
 
Or I make an Youtube video about filling my sleeping room with natural gas and venting it before I go to bed...(Shouldn't switch the light on...)
 
martinbayer said:
How about reversing the "condom" idea and instead use bladder thanks in the living area that deflate/collapse as they are depleted, potentially supported by atmospheric overpressure in the compartment(s). With such an arrangement there is no need to invert the flexible tank inside out or remove a bulkhead. With some residual propellant in gaseous form at room temperature, you might even have a ready made "air" mattress :). A challenge would be finding a bladder fabric or other material that maintains flexibility at low fuel temperatures.
Click to expand...

Sorry, I didn't get the idea at first glance, yes this would be a good alternative for fearsome pilots. Note that even the NASA had the idea of building habitats out of fuel tanks in space, it wasn't done because of a large number of surplus Saturn 6 at the time.

I really would be intrested in discussion the idea of using a glider configuration for maximum efficiency but the sleeping compartment gets all the attention...
 
Nicknick said:
So here is my idea, a kind of fixed wing glider. For obvious reasons, a ultra-long range plane should have a maximum relation of fuel mass vs. empty mass so we need to build it as light as possible. The lightest existing structures for motorized flights are in fact Paragliders. The suspension allows to eliminate almost any bending in the wing, so that it can be inflatable. I wouldn‘t go so far, since those wings are not very effective, so I would like to keep the suspension but with a reduced number of wires and use a fixed wing with an extreme wingspan. The suspension wires will cause some drag but reduce the wing bending moment to a minimum. A combination of fixed struts in the upper part and flexible wires in the lower part is also possible.

A glider design would also allow gravity control which simplifies the wing structure since no flaps are used. The stability in gliders can be achieved without a downforce producing tail, the CG is in front of the center of lift and the opposing moment is induced by the thrust and the drag of the wing (showed in the pics).

The take-off will be quite tricky, I would prefer to start and land on a frozen lake, so that runners can be used instead of wheels which saves space and weight. Also, the runway length can be much longer than for any regular runway and the cold temperatures will also help. For the start, the wing should initially be attached to the fuselage by a strut and released when the speed is increasing. The wires need to be wound up on a drum and slowly getting released to bring the wing in the flying position (shurly not an easy task…). I admit, I haven’t found a solution which I really like so far…

The fuel (mainly LNG) will be stored in the fuselage. As said, some compartments of the fuselage will be filled with liquid Methane before they are emptied and used for other purposes. This could be the sleeping compartment, the high altitude cooling system, the storing room for retractable runners or wheels and maybe even a toilet.

The compartment is fully pressurized (including the tanks and maybe even the engine compartment shall be able to act as a rescue boat or shelter in case of an emergency landing. In case of an emergency situation, the wing should be detached and a rescue parachute shall be used. Also a fast release system for the fuel will be recommended.

A combined adjustable pre swirl and rudder device is foreseen to enable a highly variable plane speed and rudder control without an additional rudder. The actuation of the pre swirl device is quite complex, maybe the best way is to control each blade by an individual electric motor.

To match my graph, I estimate a starting weight of 11 t and an empty weight of 2.5 t which is the same ratio as Burt Rutans voyager, but I have no experiences at all in airplane design, so this is just guessing. I believe, the structural weight could be lighter than that of the voyager, but the pressurisation and robust fuselage design will add some weight.

View attachment 710418View attachment 710419
Click to expand...
Please look at the latest para-gliders and competition parachutes.
As seen from the front, they have elliptical anhedral which is mainly for structural reasons.
In comparison, your semi-rigid rectangular wing would need high internal pressure to maintain its shape. You would probably need to bleed engine air up to the wing to maintain those high internal pressures.
The greater the internal pressure, the fewer external bracing wires needed.

Secondly look at recent competition parachutes (pond swooping) and sailplanes to understand their Schumann planform which has an elliptically tapered leading edge and a trailing edge that is straight or gently elliptically tapered. Schumann helps push wing tip vortices outboard and minimize the pressure differential (bottom to top) the minimize induced drag (aka. drag induced when producing lift).
 
I think I expressed my self the wrong way, with glider configuration I meant the single wing with a low mounted fuselage and propeller and not a flexible wing. The advantage of the prop pushing far below the wing is, that you can archieve stability (CG in front of center of lift) without a tail which would otherwise produce downforce and drag. The prop in conjunction with the resistance of the wing will produce the balancing moment.

My idea was using a solid carbon fibre wing with a simple structure. It might be possible to rely on shifting the CG instead of using flaps, on the other hand, the struts will become more complicate and airlerons could help to control the plane more safely.

So more struts are beeing used, so lighter the wing or so more wingspan can be realized. On the other hand, the struts will cause significant drag, so that a compromize has to be found.

The idea of using internal pressure is intresting, the Goodyear Inflatoplane allways facinated me. It could be an option to use a pressurized carbon fibre tube as wing spar, this would keep the fibres under tension and prevent buckling.

My model was done very quikly the wing shape is therefor very simple. According to my understanding, the Schuman planform is a half eliptical wing which combines the advantage of an eleptical wing (lift distribution) with a streight trailing edge. We had the Prandl II wing concept mentioned here several times which might be a better alternative:

https://www.secretprojects.co.uk/th...earch-aerodynamic-design-to-lower-drag.26806/

but this would only work out, outside of the last attachement points. In between the equations are no longer valid, because the bending moment inside the wing will be totally different.
 
Last edited:
Seems like you could use a combination of elastic and collapsing technologies to hold liquid and gas fuels at takeoff, and as the load gets burned off the external drag decreases. The living quarter can start out fully collapsed. So that internal living space may be the first tank to burn off, so very little reason to worry about cleaning up when the fuel has no direct exposure to that volume of internal space. And there is no reason not to maximize use of thin solar skins during daylight hours. Your mission profile would need to maximize sunlight. On the same token, radiant membranes can be used to cool engine and perhaps liquid gas fuels, to minimize fuel volume.
 
When the airplane takes off, it will be loaded with fuel to the absolute maximum, therefore an increased drag would be critical. Again, Methan is not a poison and it boils off without residues, so a bit venting would be totally sufficient.

The idea with the solar panals is solid, with a large wing, the additional power of the cells in combination with a mildly hybridiszed engine could increase range. The electric motor could also help with the take off by a short overboosting its power.
 
@Scott Kenny : completely off topic and it might be concealed, but in case you might answer, are subs still using compressed air to empty their ballast tanks? I mean, I can understand the advantages (no electricity needed, fool prove to use, highly reliable…), but the space and weight added to a sub is immense, isn’t it?
 
Nicknick said:
@Scott Kenny : completely off topic and it might be concealed, but in case you might answer, are subs still using compressed air to empty their ballast tanks? I mean, I can understand the advantages (no electricity needed, fool prove to use, highly reliable…), but the space and weight added to a sub is immense, isn’t it?
Click to expand...
Yes and no. Yes, the EMBT blow and high pressure blow systems use compressed air, but the preferred way is to just use some really big low pressure blowers (think roots superchargers the size of a small car). Space needed isn't terrible when you use 4500psi air tanks, and sometimes the air tanks are physically inside the ballast tanks anyways. And/or the air tanks are stuffed into the space between the ribs on a sub, which is basically dead space anyways. Those tanks are cylinders bent into a giant ( shape.

And subs need high pressure air for other things, like keeping the hydraulics pressurized, anyways. Just pray you never have to totally empty the 4500psi air supply. Takes forever to refill!
 
Some more insane ideas... (my new job bores me somewhat...)

I came across those wires used for yachts:


yachtracing.life

Future Fibres: Windswept and interesting... | Yacht Racing Life

Future Fibres: Windswept and interesting
yachtracing.life yachtracing.life


View: https://www.youtube.com/watch?v=hs7QclssZj8&ab_channel=FutureFibres


Those wires could be used for the bracing of the wing, but there is still the issue with the start. Once in the air, all cables will be kept under tension and hopefully not start to vibrate (this can hopefully be eliminated by the elliptical shape). So how, can we keep the wing up before the aerodynamic lift will take over? We need a thin long support structure which doesn’t buckle and can be removed after the takeoff. The only thin, long structures which don't buckle are pressurized hoses, which also have the advantage, that they can be rolled in after usage. A fire fighter hose B-type hose with an inner diameter of 75 mm weights 0,7 kg/m and is usually pressure tested with 25 bar, which means it could carry 1.1 t (https://www.schlauch-profi.de/Feuerwehrschlauch-DIN-14811/9230050). Two of these hoses could be guided (guiding is required for safe pressure relieve during flight) by the inner wires and hold the wing in position for the takeoff.

The wing itself can be very light, since it doesn’t contain fuel and has no flaps, so that it should nor exceed more than a ton of weight.

One thing I haven’t figured out yet, is how a weight shifting control with low drag could be applied, but this could surly be solved somehow…
 
Last edited:

Similar threads

Back
Top Bottom