- Joined
- 11 February 2010
- Messages
- 1,540
- Reaction score
- 2,293
Greetings.
I believe everyone here already familiar with this

The thing is that it seems there are bit of confusion on what to make of those decibel values or how they "define" sensitivity.
To start with.
Radar receiver sensitivity or in radar textbook known as "MDS" or "Minimum Detectable Signal". This is product of the noise "temperature" of the receiver, losses during receiving process, the thresholding process (the "SNR" part or in K Barton's book is "D(x)" or Detectability factor, the D(x) is more thorough concept than SNR as it involves losses and pulse integrations not usually included in typical Radar Range Equation (RRE)) Some authors added B or receiver bandwidth which have to match the emitted pulse or entirely discarded in RRE.
The value have big negative decibel numbers e.g -121 dB or even smaller. While the numbers for the AMDR is positive. These numbers are clearly not based on MDS nor power aperture product.
so what to make of that numbers and more importantly how do one can get or measure the number by him/herself ?.
My findings so far revealed kind of (at least for me) a concept called "Loop Gain". This is from Andy Harrison's "Introduction to Radar using Python and MATLAB" 2019 edition.

It has unit of sqm, BUT for US radar it appears imperial unit is preferred. Decibel value appears to also be used.
It is basically a concept based on signal strength achieved against a reference target and at a reference range. e.g a Radar is capable of detecting a 2 sqm RCS of Reference target at 500 Km, with measured signal to noise ratio of 24 dB. The radar's "sensitivity" is then calculated as follows :
C=500000^4*251.2/2
C=7.85 x 10^24 Sqm
In decibel it will be 249 dB. The radar is then have "Sensitivity" of 249 dB.
Now how we can apply above concept for SPY-1 and then AMDR ? First we will need to have :
-Baseline range for the AEGIS particularly calculated one.
-a reference target which for this case i use 2 sqm as that's the value seems to often be used in testing volume search radar
The calculated value is then used to compute the range and then Loop gain for the SPY-1. The following is my result :

The baseline SPY-1 in my calculation yield range of about 281 km against a 2 sqm target. Now applying the concept of Loop gain above, we can find the "Sensitivity" of the SPY-1 to be 239 dB.
How it would compare to AMDR Radar ?
First is of course we would need to find the power of the AMDR. The 9 RMA variant offers 0 dB means it will be equivalent to baseline SPY-1. This indicates it would have similar emitted power. One can assume it would have exactly 58 KW of average power. With each RMA contain about 144 TRM's this will indicate that the 9 RMA variant would have 1296 TRM in total, where each TRM will shoulder about 58/1296 = 45 Watt of average power.
In case someone wonder why i use the average power is that because for range calculation, average power gives the better indication for calculations as it directly relates on how much power overtime the radar is emitting. Higher average power means the radar sends more power overtime (higher duty cycle). While high peak power only indicates the "peak" power being emitted in each pulse but might neglect the fact that the radar is not sending as much as one having higher duty cycle. The discussion on duty cycle however is beyond the subject of this thread.
Now we have the baseline numbers we can then form a table to calculate the AMDR's loop gain and conversly compare it with our SPY-1 baseline. Which resulted in following.

The improvements are simply the number of the Loopgain in AMDR subtracted by SPY-1 Baseline and as one can see. I think it's close enough to the what depicted in the first image in this thread. Notice the 37 RMA version have "+15 dB Improvements" with 2dB margin means that it has 17 dB of total loop gain improvements while the calculated result shows 18 dB which about 1dB of error. Similarly with the 69 RMA version.
But more than that. Does it also correlates to range ? The answer is yes. The following is another table depicting my estimates of range of AMDR vs 2 sqm target.

Raytheon claims that 37 RMA can see target Half the size of baseline SPY-1 in twice the range, meaning that it's range against 1 sqm target or any reference target they might used is twice the range of the baseline SPY-1. As one can see in above target the 37 RMA version can see same sized target 3 times than baseline SPY-1 and 2.43 times for half sized target, which i think close enough to "2" times with margin. The 69 RMA can see same target 5 times more while half sized one are 3.87 times more or about close to 4 times as claimed.

The range factor and therefore range here is calculated based on the "0dB" improvements which essentially the baseline SPY-1. One can easily calculates range of AESA radar based on the number TRM with 4th root.

Note that the above assumes only increase in number of TRM. additional variables like if one wish to vary the power etc.. have to be added.
Guess that's all i think. One can use the loopgain equation to actually calculates angular measurement accuracy/miss distance of a radar against targets in specified range. One application is to maybe answering question on "what distance x radar have enough accuracy to support gunfire ?"
Another thing i noticed is that this measure of "sensitivity" appears to not be used outside of the United States. Thus this might only be useful to compare US made radar with another US made radar. Another limitation is it might only be used to compare the baseline radar with its deriviative. One cannot use measure of loop gain to compare e.g AN/MPQ-53 with AN/SPY-7 but instead it can be used to compare AN/MPQ-53 to AN/MPQ-65 and maybe its much later deriviatives the GaN based new Patriot radar.
I believe everyone here already familiar with this
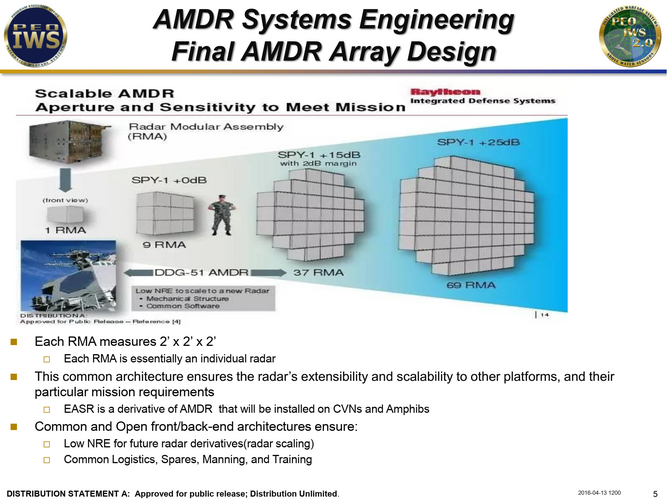
The thing is that it seems there are bit of confusion on what to make of those decibel values or how they "define" sensitivity.
To start with.
Radar receiver sensitivity or in radar textbook known as "MDS" or "Minimum Detectable Signal". This is product of the noise "temperature" of the receiver, losses during receiving process, the thresholding process (the "SNR" part or in K Barton's book is "D(x)" or Detectability factor, the D(x) is more thorough concept than SNR as it involves losses and pulse integrations not usually included in typical Radar Range Equation (RRE)) Some authors added B or receiver bandwidth which have to match the emitted pulse or entirely discarded in RRE.
The value have big negative decibel numbers e.g -121 dB or even smaller. While the numbers for the AMDR is positive. These numbers are clearly not based on MDS nor power aperture product.
so what to make of that numbers and more importantly how do one can get or measure the number by him/herself ?.
My findings so far revealed kind of (at least for me) a concept called "Loop Gain". This is from Andy Harrison's "Introduction to Radar using Python and MATLAB" 2019 edition.

It has unit of sqm, BUT for US radar it appears imperial unit is preferred. Decibel value appears to also be used.
It is basically a concept based on signal strength achieved against a reference target and at a reference range. e.g a Radar is capable of detecting a 2 sqm RCS of Reference target at 500 Km, with measured signal to noise ratio of 24 dB. The radar's "sensitivity" is then calculated as follows :
C=500000^4*251.2/2
C=7.85 x 10^24 Sqm
In decibel it will be 249 dB. The radar is then have "Sensitivity" of 249 dB.
Now how we can apply above concept for SPY-1 and then AMDR ? First we will need to have :
-Baseline range for the AEGIS particularly calculated one.
-a reference target which for this case i use 2 sqm as that's the value seems to often be used in testing volume search radar
The calculated value is then used to compute the range and then Loop gain for the SPY-1. The following is my result :
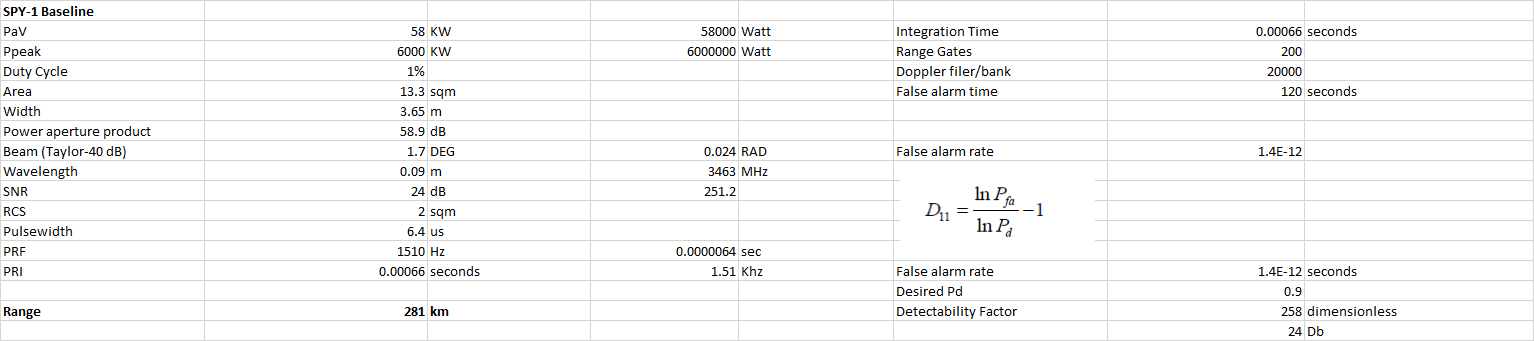
The baseline SPY-1 in my calculation yield range of about 281 km against a 2 sqm target. Now applying the concept of Loop gain above, we can find the "Sensitivity" of the SPY-1 to be 239 dB.
How it would compare to AMDR Radar ?
First is of course we would need to find the power of the AMDR. The 9 RMA variant offers 0 dB means it will be equivalent to baseline SPY-1. This indicates it would have similar emitted power. One can assume it would have exactly 58 KW of average power. With each RMA contain about 144 TRM's this will indicate that the 9 RMA variant would have 1296 TRM in total, where each TRM will shoulder about 58/1296 = 45 Watt of average power.
In case someone wonder why i use the average power is that because for range calculation, average power gives the better indication for calculations as it directly relates on how much power overtime the radar is emitting. Higher average power means the radar sends more power overtime (higher duty cycle). While high peak power only indicates the "peak" power being emitted in each pulse but might neglect the fact that the radar is not sending as much as one having higher duty cycle. The discussion on duty cycle however is beyond the subject of this thread.
Now we have the baseline numbers we can then form a table to calculate the AMDR's loop gain and conversly compare it with our SPY-1 baseline. Which resulted in following.

The improvements are simply the number of the Loopgain in AMDR subtracted by SPY-1 Baseline and as one can see. I think it's close enough to the what depicted in the first image in this thread. Notice the 37 RMA version have "+15 dB Improvements" with 2dB margin means that it has 17 dB of total loop gain improvements while the calculated result shows 18 dB which about 1dB of error. Similarly with the 69 RMA version.
But more than that. Does it also correlates to range ? The answer is yes. The following is another table depicting my estimates of range of AMDR vs 2 sqm target.

Raytheon claims that 37 RMA can see target Half the size of baseline SPY-1 in twice the range, meaning that it's range against 1 sqm target or any reference target they might used is twice the range of the baseline SPY-1. As one can see in above target the 37 RMA version can see same sized target 3 times than baseline SPY-1 and 2.43 times for half sized target, which i think close enough to "2" times with margin. The 69 RMA can see same target 5 times more while half sized one are 3.87 times more or about close to 4 times as claimed.

The range factor and therefore range here is calculated based on the "0dB" improvements which essentially the baseline SPY-1. One can easily calculates range of AESA radar based on the number TRM with 4th root.

Note that the above assumes only increase in number of TRM. additional variables like if one wish to vary the power etc.. have to be added.
Guess that's all i think. One can use the loopgain equation to actually calculates angular measurement accuracy/miss distance of a radar against targets in specified range. One application is to maybe answering question on "what distance x radar have enough accuracy to support gunfire ?"
Another thing i noticed is that this measure of "sensitivity" appears to not be used outside of the United States. Thus this might only be useful to compare US made radar with another US made radar. Another limitation is it might only be used to compare the baseline radar with its deriviative. One cannot use measure of loop gain to compare e.g AN/MPQ-53 with AN/SPY-7 but instead it can be used to compare AN/MPQ-53 to AN/MPQ-65 and maybe its much later deriviatives the GaN based new Patriot radar.
Last edited:
